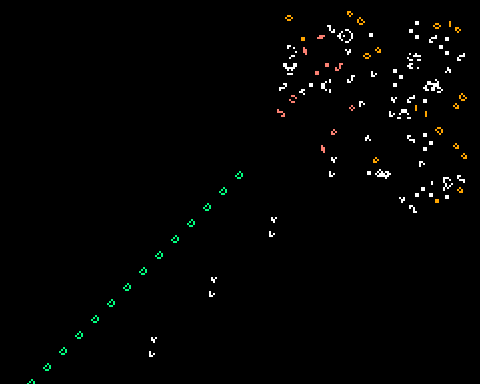
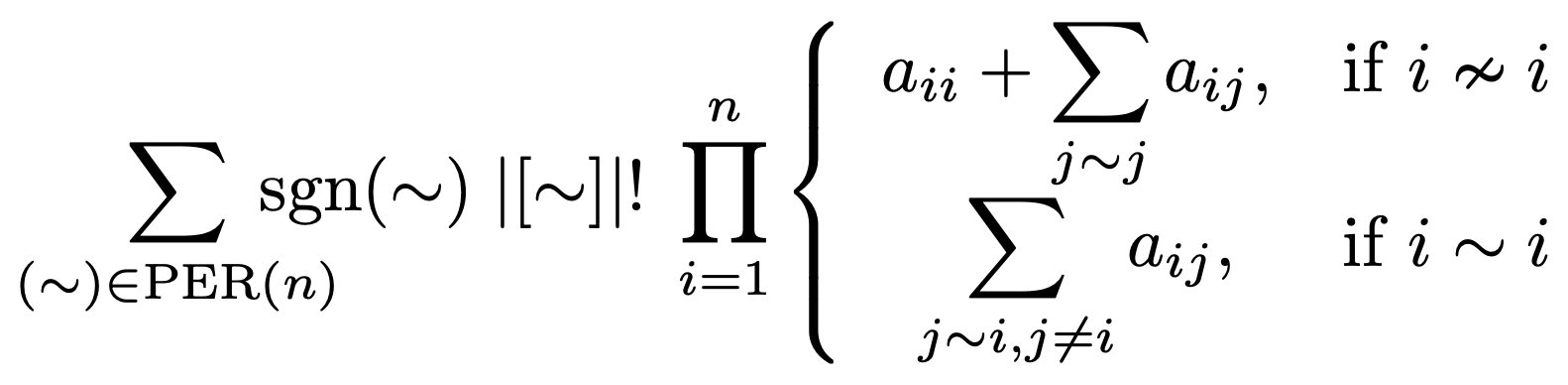A phoenix is an oscillator in Conway’s Life where every cell dies in every generation. The smallest example is Phoenix 1, which oscillates with period 2 and has a constant population of 12:

All known finite phoenices have period 2, and Stephen Silver proved in 2000 that there cannot exist a finite phoenix of period 3. Alex Greason more recently proved the non-existence of any phoenix (finite or infinite) with period 3 or 5.
Infinite phoenix agars (patterns that are periodic in two directions, filling the whole plane) and wicks (patterns that are periodic in one direction) are known for certain larger periods; the forum user wwei23 recently showed the existence of phoenix wicks of all periods divisible by 6:

Construction by wwei23 showing the existence of phoenix wicks of all periods of the form 6n
It seemed as though a finite period-4 phoenix may have been possible, as Keith Amling found period-4 wicks consisting of a narrow flexible rope supported by finite period-2 supports:

Keith Amling’s flexible period-4 wick
In particular, if it were possible to bend this around somehow into a closed loop, then we would have a finite period-4 oscillator. After trying in vain for a long time to find one, it became increasingly plausible that no such oscillator exists. Eventually it was possible to prove the non-existence of finite phoenices of periods between 3 and 69, and eventually prove the non-existence of finite phoenices of any period other than 2. The proof is computer-assisted, making use of SAT solvers to automate finite case-bashes (much like Alex Greason’s disproof of p3 and p5 phoenices), but the overall structure of the proof is quite simple and human-comprehensible.
Preliminaries
Before we begin the main proof, we will establish facts about finite phoenices which help to accelerate the SAT solver by reducing the search space that it needs to explore. These facts will also be proved with the help of a SAT solver, but obviously for the avoidance of circularity we cannot assume these facts until they have been proved. In particular, the overall structure of the proof will look like:
- A: only 11 of the 16 possible 2 × 2 squares can occur in a finite phoenix;
- B: only 99 of the 512 possible 3 × 3 squares can occur in a finite phoenix;
- C: every finite phoenix has period 2;
where we assume A when proving B, and assume B when proving C.
Suppose that we have a finite phoenix oscillator. We say that a 2 × 2 square of cells is heavy if there is some time T where at least three of the four cells in that square are live. We show that no heavy squares can exist by the following argument:
- Suppose there exists such a heavy square [x, x+1] × [y, y+1];
- With out loss of generality, suppose that (x, y) is maximal, with respect to the lexicographic ordering on Z^2, over all such heavy squares (we can do this because the oscillator is finite by assumption);
- Let T be a generation for which the heavy square contains at least three live cells, and then consider the 16 × 16 × 8 box of cells (the 16 × 16 neighbourhood centred on the heavy square, from time T − 5 to T + 2);
- Create a Boolean variable for each cell together with constraints specifying that the Life rules are followed, that every live cell dies in every generation, and that there is no heavy square [u, u+1] × [v, v+1] such that (u, v) is lexicographically greater than (x, y);
- Feed the resulting constraints into a SAT solver and derive a contradiction.
Now that we have established that no heavy squares can exist, we can feed this in as an additional constraint to speed up subsequent SAT problems. The next thing that we do is determine the set of possible 3 × 3 neighbourhoods that can occur at some generation in a finite phoenix: we find that of the 512 possible neighbourhoods (102 up to symmetry), only 99 of these (22 up to symmetry) can occur; they were originally tabulated by forum user wwei23 here. (Apparently wwei23 was able to establish this for all phoenices, finite or infinite, with the sole exception of the Venetian blinds agar.)
These neighbourhood constraints can again be injected into any SAT problems to accelerate the search. Specifically, we combine the Life rules with these neighbourhood constraints to obtain, for every 10 cells consisting of a 3×3 neighbourhood at time t together with the central cell at time t + 1, a proposition in these 10 Boolean variables whose 1024-element truth table consists of 99 true values and 925 false values. We encode this proposition by specifying all minimal clauses that are implied by this proposition, the set of which can be determined by an algorithm by Eugenio Morreale described in the solutions to exercises 29 and 30 from 7.1.1 of Knuth’s TAOCP.
The code for proving these preliminary lemmata is here.
The main proof
Suppose that we have a finite phoenix of period greater than 2. We define the extremal cell to be the cell (x, y) with the following properties:
- The cell (x, y) oscillates with period greater than 2;
- The value x + y is maximum amongst all cells with this property;
- The value y is maximum amongst all cells with these properties.
By definition, any other cell (u, v) with u + v > x + y or with u + v = x + y and v > y will necessarily be either constantly off or oscillate with period 2.
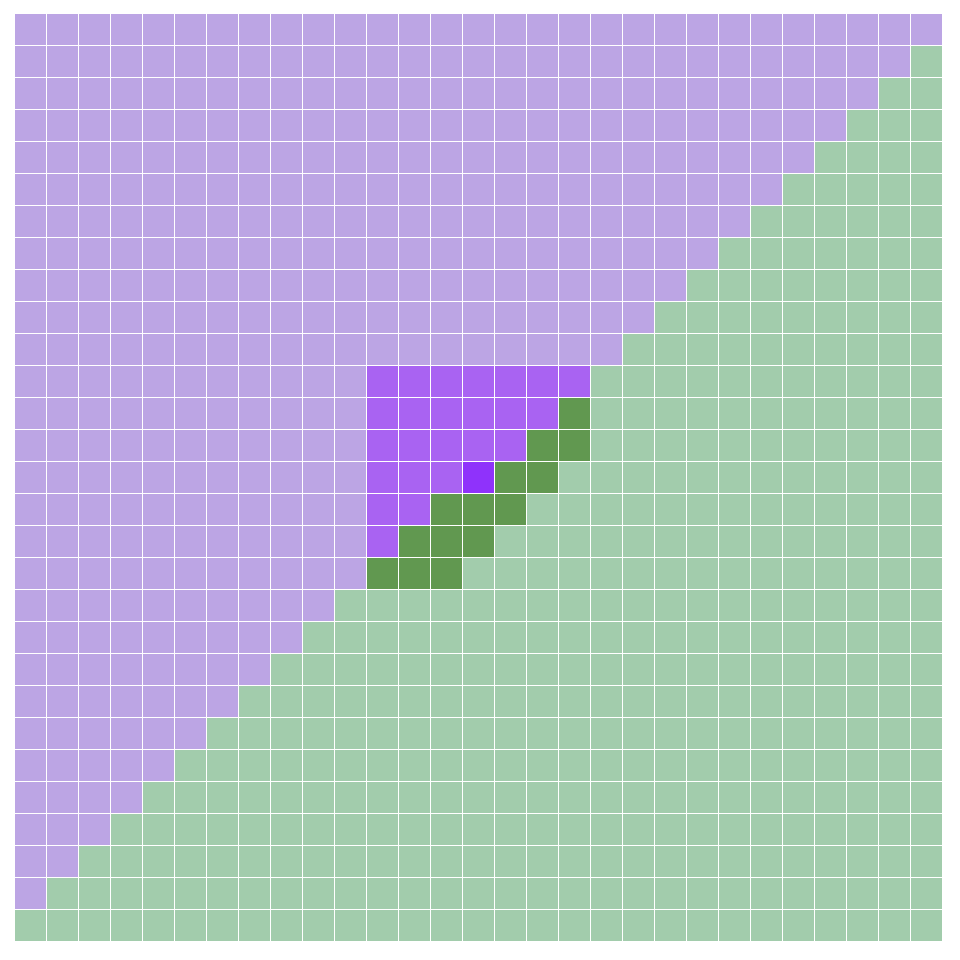
In the diagram above, we show the extremal cell in deep purple and the surrounding 29 × 29 neighbourhood. The forced-vacuum-or-p2 cells are shown in green; the cells that are allowed to be higher period are shown in purple. We also highlight a 39-cell patch centred on the extremal cell; this will be important later in the proof.
As the central cell oscillates with period greater than 2, there must be a time T for which the central cell is off at time T and on at time T+2. We now consider the 29 × 29 × 32 box of cells (the 29 × 29 neighbourhood from time T − 17 to T + 14) and create a Boolean variable for each cell; to these 26912 variables we introduce the following constraints:
- every 3 × 3 neighbourhood is one of those that can appear in a phoenix, and the Life rules are obeyed;
- if (u, v) is in the green region, then the variables (u, v, t) and (u, v, t+2) are equal;
- the central cell (x, y, T) is off and (x, y, T+2) is on.
We then run an incremental SAT solver (Armin Biere’s CaDiCaL) on this problem to find all possible values of the 39-cell patch at time T. It transpires that there are 20 such possibilities for the patch:

For each of these patches, we create a new SAT problem, again on a 29 × 29 × 32 box of cells (albeit shifted 2 generations backwards in time), and search for all patches that can occur 2 generations before each of these patches. Ignoring the patches above, there are a further 20 distinct patches that can occur:

We can keep repeating this process, forming a breadth-first traversal of the directed graph of possible 39-cell patches that can occur at times T − 2k in the ancestry of the central cell. We find 46 more patches in the next layer, then 35 in the next, then 5, 6, 20, 28, 13, 4, and finally 0. At this point, we have traversed all of the possible 39-cell patches (197 in total).
For all of these 197 possible patches, the central cell is off, which means that there’s no time T − 2k which matches the state at time T, so we cannot have a periodic phoenix. (In particular, if we had a phoenix of period p, then it must be identical in generations T − 2p and T, thereby obtaining a contradiction.)
It therefore follows that every finite phoenix has period 2.
When I ran the program to enumerate the possible patches, I also tracked the full directed graph that contains a vertex for each of the 197 patches and a directed edge whenever a patch can be the grandparent of another patch. The reason for doing this is that I didn’t know a priori that all of the patches would have central cell off, leading to an easy proof; instead, I thought that it might be the case that some had central cell on, but that there’s no directed cycle containing such a vertex (a weaker condition, but still sufficient for the proof).
The graph has 197 vertices, 1017 edges, and 10 connected components, but there’s no obvious structure beyond that:

Corollaries
In any case, the fact that every finite phoenix has period 2 leads to the corollary that every phoenix has constant population: if it’s infinite, then the population is ℵ_0; otherwise, the oscillator is finite (therefore p2) and we can consider the (disjoint) sets A and B, where A is the set of cells alive at even generations and B is the set of cells alive at odd generations. Every cell in A has exactly 3 neighbours in B, and every cell in B has exactly 3 neighbours in A, so the sets have equal size.
(The p2 part of this proof was done much earlier by the forum user Praosylen who looked at the 3-regular bipartite graph with vertex-classes A and B and an edge whenever two cells are adjacent, and proved other properties such as bridgelessness. All of this research now applies to all finite phoenices, since non-p2 finite phoenices have been ruled out.)