This article was originally supposed to be about TREE(3) and the busy beaver function. However, I realised the potential of turning TREE(3) into a two-player finite game, which is surprisingly fun and means that I’ve ended up leaving uncomputable functions until a later post.
Last time, we explored a fast-growing hierarchy of functions. We considered the Goodstein sequence (or rather, the essentially equivalent problem C8′) to produce a function approximately equal to f_(ε_0), where ε_0 is a rather large countable ordinal. Applying this construction recursively would correspond to ordinals such as ε_0 + ω, which are not much larger than ε_0. So, if we want faster functions, we need more powerful ideas.
Friedman’s TREE(3)
Usually, we expect fast-growing functions to have a relatively smooth, steady start. For instance, the Ackermann function begins {3, 4, 8, 65536, 2↑↑(2↑↑65536), …}, and the first four terms are quite small. By contrast, the function TREE begins with TREE(1) = 1, TREE(2) = 3 and TREE(3) is so vastly, incredibly large that it greatly exceeds anything you can express in a reasonable amount of space with iteration, recursion and everything else mentioned in the previous post, including C8′ and the Goodstein function.
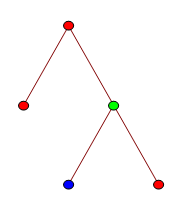
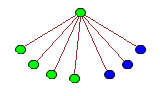
So, what exactly is TREE? The definition is quite simple, once we’ve defined a few terms along the way. We consider rooted k-labelled trees, which are connected acyclic graphs where one vertex is identified as the ‘root’, and each vertex can have one of k colours. An example is shown below:
There is a binary operator, inf (not related to the infimum of a set), which returns the latest common ancestor of two vertices. Consider the tree above. If the blue vertex is called x and the green vertex is called y, then x inf y = y. Similarly, the inf of the two non-root red vertices is the root vertex.
We say that a tree S is homeomorphically embeddable into a tree T if there is an injection φ from the vertices of S to the vertices of T such that:
- φ(z) and z have the same colour, for all z in S;
- φ(x inf y) = φ(x) inf φ(y), for all x,y in S.
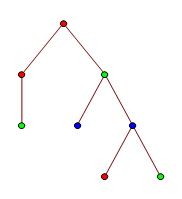
Equivalently, this means that T is a topological minor of S (where we direct the edges to respect the root vertex). The first tree is homeomorphically embeddable into this one:
Proof: Delete the two green leaves, then contract the double-edge containing a blue vertex.
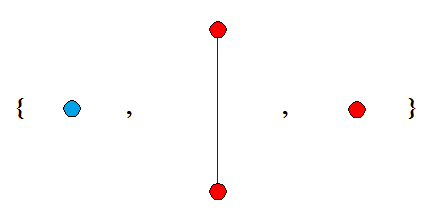
If we have an infinite sequence of k-labelled trees {T_1, T_2, T_3, …}, where each T_n has at most n vertices, then Kruskal’s tree theorem states that some T_i can be homeomorphically embedded into a later T_j. Hence, by compactness, there exists some value TREE(k), which is the length of the longest possible sequence of k-labelled trees {T_1, T_2, …, T_TREE(k)} such that |T_n| ≤ n (for all n) and no earlier tree can be homeomorphically embedded into a later tree.
The sequence above is the longest such sequence of 2-labelled trees, so TREE(2) = 3. For any sequence, the first tree must be a single isolated vertex, and that colour is not allowed to occur in any later tree. The proof follows trivially. Now consider 3-labelled trees. We can have an extremely long sequence, such as one which starts like this:
As you can see, by T_20 it’s getting difficult to draw the trees. A much more efficient notation is to use balanced parentheses:
T1 {}
T2 [[]]
T3 [()()]
T4 [((()))]
T5 ([(())][])
T6 ([(())](()))
T7 ([(())]()()())
T8 ([(())]()())
T9 ([(())]())
T10 ([(())])
T11 [(())]
T12 ([()][()][()][()][()][])
T13 ([()][()][()][()][()](()))
T14 ([()][()][()][()][()]()()())
T15 ([()][()][()][()][()]()())
T16 ([()][()][()][()][()]())
T17 ([()][()][()][()][()])
T18 ([()][()][()][()][][][][][][][][][])
T19 ([()][()][()][()][][][][][][][][](()))
T20 ([()][()][()][()][][][][][][][][]()()())
T21 ([()][()][()][()][][][][][][][][]()())
T22 ([()][()][()][()][][][][][][][][]())
T23 ([()][()][()][()][][][][][][][][])
...
A related function, tree, asks for the longest sequence {U_1, U_2, …, U_tree(r)} of 1-labelled trees such that |U_n| ≤ n + r (for all n) and no tree is homeomorphically embeddable into a later tree. By extending the sequence shown above, it can be proved that TREE(3) has the following (weak) lower bound:
Proof (added 2020-07-24 in response to surprisingly hostile claims that I never had a proof of this bound): After the sequence described above, one can create a new tree, T24, which is of the form:
T24 ([()][()][()][()][][][][][][][]X7)
where X7 is any (monochromatically green) tree on 7 vertices. This can be followed by the sequence:
T25 ([()][()][()][()][][][][][][][]X8) T26 ([()][()][()][()][][][][][][][]X9) T27 ([()][()][()][()][][][][][][][]X10) ...
where X7, X8, X9, X10, … is a maximal-length sequence for tree(7). At the end of this process, we have:
T_(23 + tree(7)) ([()][()][()][()][][][][][][][]())
as () is necessarily the last element of the maximal-length sequence for tree(7). We can then extend the sequence further by ‘burning’ another blue node:
T_(24 + tree(7)) ([()][()][()][()][][][][][][][]) T_(25 + tree(7)) ([()][()][()][()][][][][][][]Y1)
where Y1 is the first tree in the maximal-length sequence for tree(tree(7)). We proceed in the same way as before with a sequence of tree(tree(7)) terms, culminating in:
T_(23 + tree(7) + tree(tree(7))) ([()][()][()][()][][][][][][]()) T_(24 + tree(7) + tree(tree(7))) ([()][()][()][()][][][][][][]) T_(25 + tree(7) + tree(tree(7))) ([()][()][()][()][][][][][]Y2)
where Y2 is the first tree in the maximal-length sequence for tree(tree(tree(7))). Repeating this process, we eventually reach the tree:
([()][()][()][()])
at time 24 + tree(7) + tree(tree(7)) + … + tree^8(7). We can then make the next tree in our process have the form:
([()][()][()][][][][][]...[]X7)
where we have created tree^8(7) new blue nodes by ‘burning’ a branch of the form [()]. The same argument as before allows us to reach the tree:
([()][()][()])
at time well beyond tree^(tree^8(7))(7). Repeating this outer iteration another three times gets us to the claimed bound.
To see that no tree embeds homeomorphically into a later tree, we note that if T precedes T’, then we have at least one of the following:
- T contains more copies of [()] than T’;
- T contains more copies of [] than T’;
- The monochromatic green subtree of T precedes the monochromatic green subtree of T’;
where the latter condition was ensured by using a sequence for tree(k) which has this property by definition.
The result follows. QED
The game of Chomp
For a quick and refreshing detour from large numbers, we’ll consider the game of Chomp. We begin with a rectangular chocolate bar of size m by n, the bottom-left corner of which has been laced with cyanide.
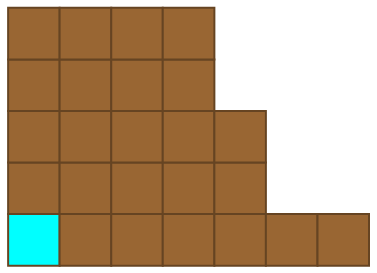
Players alternate turns, eating a square of chocolate together with everything above and to the right of it. For instance, after the first move the resulting configuration might resemble this:
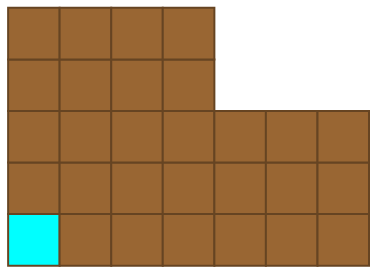
Then, the second player responds:
This continues until some unlucky person is left with the cyanide-laced square of chocolate and endures a slow, painful death. Who has the winning strategy? Without explicitly constructing a winning streategy, it’s possible to prove that the first player can force a win through an argument known as strategy stealing.
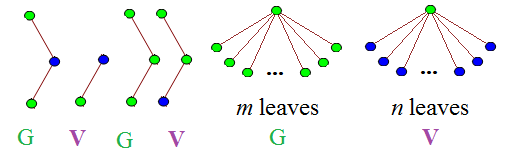
Assume that the second player has a winning strategy, with the intention of deriving a contradiction. Let the first player (I generally use Gabriel and Vishal as example names in combinatorial game theory, and we’ll use alphabetical order, so Gabriel) eat the top-right square of chocolate:
Now, Vishal has a winning strategy at this point. Let’s assume (without any real loss of generality) that he can force a win by making this move:
Gabriel could have made this move to begin with, so Vishal can’t possibly have a winning strategy. Reductio ad absurdum. As the game cannot terminate in a draw, we conclude that Gabriel has the winning strategy. This proof is heavily non-constructive, and no-one knows what this winning strategy is for arbitrary positive integers m,n.
Chomp is called an impartial game, since the same moves are theoretically available to each player, and it just depends on whose turn it is. Nim is another example. Both of these can be expressed as poset games, where players take turns to remove any element of a partially-ordered set together with all greater elements.
Making a game out of TREE(3)
That was a well-deserved distraction, but let’s return to TREE(3). We can define a two-player impartial game (which is, incidentally, a poset game) with the following rules:
- Players alternate taking turns.
- On the nth turn (odd for Gabriel, even for Vishal), each player draws a 3-labelled tree with at most n vertices.
- If you draw a tree such that an earlier tree is homeomorphically embeddable into it, you lose.
By definition, such a game lasts at most TREE(3) turns and can never result in a draw. I don’t know what the parity of TREE(3) is, so I don’t know who wins the longest game. Indeed, I don’t even know which player has the winning strategy in TREE(3), and an exhaustive search is impractical. [Edited 2020-08-21: unfortunately, there’s a trivial winning strategy for the first player; after playing a single red vertex, respond to every move by your opponent by simply playing your opponent’s last tree with the colours blue and green reversed. An analogous game on subcubic graphs would be more interesting.]
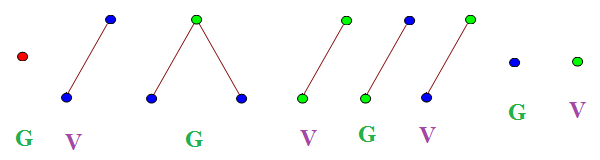
An example game is this one, which Vishal wins after 8 turns:
Believe it or not, all reasonably-sized games of Chomp can occur as positions in natural games of TREE(3). Firstly, we return to the previous scheme for getting really long sequences:
Now, we can continue this for a very long time (x moves, where x has this unimaginably large lower bound):
After this incredibly long sequence of moves, the next six moves might be these (let m and n be positive integers where m + n < x; in practice, x is so large that it is unrestrictive):
This might not seem like a particularly poor move on Vishal’s part, but it transpires that Gabriel now has a definite winning strategy. If a player plays a single vertex (blue or green, since red was exhausted on the first move), the opponent can win by playing the single vertex of the other colour. Also note that no blue node can have a child, and no tree can have a depth more than three. In other words, subsequent moves resemble this:
This particular move is abbreviated to (4,3). Due to the ‘forbidden’ trees which appeared first, all moves must be of the form (a,b), where a < m and b < n. Interpreting these as coordinates, you may notice that this is precisely emulating the game of Chomp on a m by n grid! Exciting!
Consequently, Gabriel can force Vishal to ultimately play (0,0), which is a single green vertex. Gabriel immediately wins by playing a single blue vertex, leaving Vishal with no legal moves.


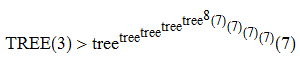


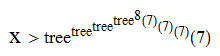
Some time ago I read that paper: ftp://ftp.cis.upenn.edu/pub/papers/gallier/kruskal1.pdf
It’s said there that Kruskal’s Theorem and Friedman’s Finite Form of it can be proven to be true by equiping ourselves with Γ_0 well ordering statement. If so, we can use it to prove that TREE function is total, without need to use ordinal as enormous as Veblen ordinal. Doesn’t that imply that TREE(x) is of order f_Γ_0(x)?
Also, you didn’t write about n(x) function 🙂
I read elsewhere (in Harvey Friedman’s notes, if I remember correctly) that the strength of Kruskal’s tree theorem is measured by the small Veblen ordinal, which is greater than the Feferman-Schütte ordinal.
As for the n() function, it was too slow-growing for this post (it’s dominated by f_(omega^3), so pales in comparison with the Goodstein function mentioned at the end of the previous post).
Uncomputable functions should follow shortly.
Ah, sorry, you are right. What paper actually said (second part of paper) is that Kruskal’s theorem implies Γ_0 well ordering, not vice versa, as I understood it. So that theorem must be strictly stronger than Γ_0 well ordering statement, thus TREE function can be such fast-growing. Sorry, my bad 😛
Pingback: Busy beavers | Complex Projective 4-Space
Friedman has also described a number called SCG(13) that is far larger than TREE(3): http://www.cs.nyu.edu/pipermail/fom/2006-April/010362.html
There’s some talk that Bird’s function is only at the level of Γ0 at most: http://forums.xkcd.com/viewtopic.php?f=14&t=7469&p=2191420
I have no idea if that’s true, however.
Also, “Deedlit” gives a nice explanation of subcubic graph numbers here: http://googology.wikia.com/wiki/Talk:Subcubic_graph_number
More specifically, he shows that SCG(0) = 6 and SCG(1) > fε04(29), and that the growth rate is at least the level of ψΩ1 (Ωω). I may be wrong, but I believe that is larger than the Bachman-Howard ordinal.
In the subsequent post ‘graph minors’, I’ve investigated values of the related function SSCG (*simple* subcubic graph numbers, where you’re not allowed multigraphs). TREE(3) is much smaller than SSCG(3), and much larger than SSCG(2):
http://cp4space.wordpress.com/2013/01/13/graph-minors/
There’s no qualitative difference between the asymptotic growth rates of SSCG and SCG. It’s clear that SCG(n) >= SSCG(n), but I can also prove SSCG(4n + 3) >= SCG(n).
Pingback: Graph minors | Complex Projective 4-Space
Has Friedman an upper bound for the number of elementary particles in the entire Universe?
In the observable universe, I seem to recall that there are about 10^80 elementary particles. In the entire (possibly infinite) universe, there are at most aleph_one (the first uncountable cardinal), assuming the following:
1. Space is locally R^3;
2. Elementary particles are open sets.
Equality occurs, for example, in the case where space is (Alexandroff line)^3 and particles are positioned in each (unit interval)^3.
Sorry, I forgot to mention that I’m also implicitly assuming the Universe is path-connected.
Might it be better to say “Ackermann function begins {3, 4, 8, 2↑↑4 (=65536), 2↑↑(2↑↑(2↑↑4)), …}”
Great article, but I’m still unclear on how Kruskal’s tree theorem implies that there is a single upper bound for all sequences of k-labelled trees without a homeomorphic embedding. The article states compactness and references the Bolzano-Weierstrass article but how do we invoke compactness here?
Consider the game-tree of all possible positions. Each node has finite degree (because there are only finitely many possibilities you can play on a given move) and there is no infinite path (by Kruskal’s tree theorem), so K\H{o}nig’s tree lemma implies that the game-tree is finite.
The restriction that on the nth turn a player must pick a tree with at most n vertices is neither necessary nor natural. The Kruskal tree theorem shows that the game must end even if the players play arbitrarily large trees. Of course, without such a rule there’s no upper bound on how the game will last, making this an infinite game. All the more fun!
Question. Does the game of tree 3 have no fate but to end up with each tree only being two generations for trillions of moves? There’s no game where you could have 10 generations? Thanks
also. Couldn’t the 12th tree instead have 12 green nodes expanding 12 generations?
Note that this no need to limit the number of vertices if your making it a game. Combinatorial game theory simply demands that every line of play is finite, not that it is bounded (see for example Sylver coinage). See https://mathoverflow.net/q/284580/65915
The sequence showing how TREE(3) might start looks wrong to me. The 4th tree is a subset of the 5th and 6th trees. The 11th tree is a subset of the 12th tree.
I think maybe what I’m missing is that there is a parent-child relationship that must be maintained? It’s not really stated anywhere, but looks like this is one of the rules. So for one tree to contain another, the parent-child ordering must also be maintained. Is that right? And presumably each node can only have at most one parent?
Actually the rule is the new tree should not contain an older tree but, an older tree can contain a new tree. Here contain means the nearest common ancestor should not be same.
Pingback: The Enormous TREE(3) – Numberphile – Деревья – легкие планеты
Pingback: TREE(3) is a big number, I mean really big. - Josh Kerr
Pingback: Fast-growing functions revisited | Complex Projective 4-Space
Pingback: El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo - ISV
Pingback: El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo
Pingback: El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo | ReportateRD
Pingback: El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo - Mirando la Hidrovía
Pingback: Xataka – El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo – Yacal
Pingback: El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo - Ocio24
Pingback: El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo – Radio Centro F.M. 97.1 Pcia. De Buenos Aires
Pingback: El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo – Radio Región
Pingback: El número TREE(3) no es infinito, pero es tan grande que ni siquiera cabe en el universo - La Fragua