In three dimensions, the familiar cross product is a bilinear function expressible in terms of the Levi-Civita alternating tensor. Specifically, a = b × c can be written as ai = εijk bj ck, which has the following beautiful properties:
- Bilinearity: a is a linear function of b (when c is fixed), and a linear function of c (when b is fixed);
- Complete antisymmetry: swapping any two of the indices flips the sign of the tensor;
- Orthogonality: a is always perpendicular to b and c;
- Isotropy: the tensor is unchanged when transformed in SO(3).
It should be evident that for orthogonality and isotropy, the cross product can only be defined in three dimensions. In two dimensions or lower, there are insufficiently many dimensions for orthogonality. On the other hand, in four or more dimensions, we can apply a rotation that preserves b and c whilst changing a, so the cross product cannot be well defined. Hence, it only exists in three dimensions (unless it is identically zero, which is stupid and trivial).
However, if we relax the condition of total isotropy, there exists a seven-dimensional analogue of the cross product. It is uniquely determined (up to automorphism of the underlying vector space) by the following conditions:
- Bilinearity;
- Complete antisymmetry;
- Orthogonality.
Even though it doesn’t have full isotropy (i.e. the automorphism group of the tensor is smaller than SO(7)), it still retains a lot of symmetry. The automorphism group is the compact real form of the exceptional Lie group G2.
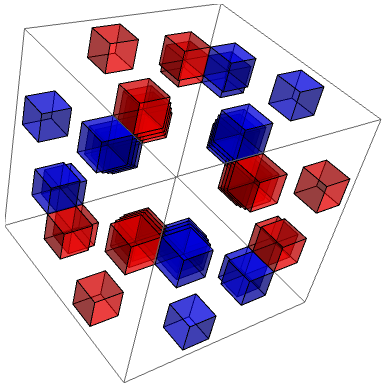
If we choose the canonical coordinate system, then the components of the tensor can be visualised as a three-dimensional array (where blue and red are +1 and −1, respectively):
The projection shown above highlights the antisymmetry of the tensor — reflecting in an axis causes the colours of the entries to alternate. Note that the position (x, y, z) is non-zero if and only if x, y and z are collinear on (a particular labelling of) the Fano plane.
Quaternions and octonions
With a slight abuse of notation, one can write a quaternion as a sum of a scalar and vector, such as λ + a, where λ is the real part and a is the (three-dimensional) imaginary part. Then, the rule for multiplying quaternions becomes:
- (λ + a)*(μ + b) = (λμ − a · b) + (λb + μa + a × b)
In fact, if we define the one-dimensional cross product to be identically zero, then this is also the definition of multiplying complex numbers. Using a seven-dimensional cross product, we obtain the rule for multiplying weird eight-dimensional entities called octonions. Whilst quaternions are slightly bad (they’re not commutative), octonions are really bad (they’re non-associative, which means you need to use parentheses in products of three or more octonions)!
There’s a book by John Conway and Derek Smith about quaternions and octonions. Rather informatively, it’s entitled On Quaternions and Octonions.
Split octonions
The (squared) norm of an octonion is defined to be the sum of the squares of its components, just as one would define the norm of a complex number. Equivalently, we can consider it to be the length of an octonion as a vector in eight-dimensional space.
It transpires that the octonions have a more pathological cousin, the split octonions, where four of the coordinates are spacelike and the other four are timelike. In other words, they live in a (4+4)-dimensional Minkowski space. When the (seven-dimensional) subspace of purely imaginary octonions is projectivised (the origin is thrown away and real scalar multiples are associated), we get a beautiful six-dimensional projective space. John Baez and Huerta discovered that this is precisely the space of positions of a spinorial ball rolling on the surface of a projective ball of three times its diameter.
Moreover, lines in this six-dimensional space are defined in a natural way, both in terms of the octonionic representation (as subplanes where all products have a norm of zero) and in terms of the rolling balls (as geodesic trajectories where the smaller ball rolls along a great circle of the larger ball).
And the symmetry group of this six-dimensional projective space? The split form of G2, naturally…
symbols, such that each n-symbol string over Σ appears exactly once. For example, taking Σ to be an alphabet of four colours and choosing n = 3 gives the following de Bruijn sequence of length 64:
. Even more impressive is that the concept generalises to de Bruijn tori, which are known to exist in the square case. For example, here is a 
torus with 2 colours and every possible 
block as a subregion:
, but larger cases are beyond the capabilities of brute-force exhaustive search.
, with an unconfirmed result giving a value of H below 5000. It’s surprising how far these sieve methods are successfully being pushed — significantly below Ben Green’s estimate that 10000 would be the limit.
and 
. If you plot c and q on the complex projective plane, the resulting surface is a topological torus; it is said to have a genus (number of holes) of 1. This means that algebraic massage can convert it into an elliptic curve. Let’s attempt this. Firstly, we want a polynomial, so the obvious step is to eliminate the denominator:
and 
. It is easy to show that we can express q and c as rational functions of x,y,n, so rational points on this elliptic curve correspond to rational right-angled triangles with area n. Assuming the Birch and Swinnerton-Dyer conjecture, the existence of rational solutions can be verified by a 
sets. So it’s really big. In general, Vn contains 
sets.
