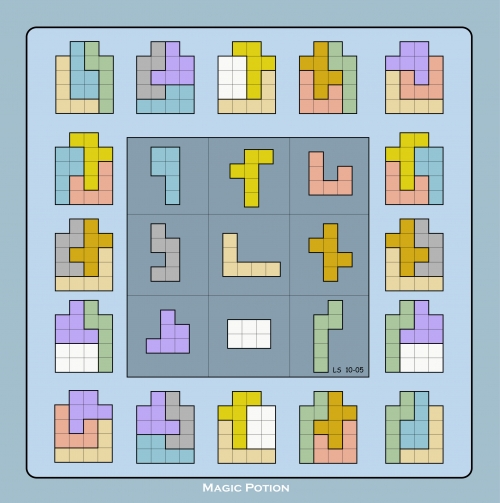
In 2001, Lee Sallows generalised the concept of a magic square, replacing the integers in each cell with subsets of the plane. He calls such a configuration a ‘geomagic square’ if the subsets in every row, column and diagonal can tile the same shape. One of my favourites is this one, where nine distinct hexominoes appear:
He has produced geometric versions of many extant magic squares (including Dürer’s square), as well as some examples which do not have non-trivial numerical analogues (e.g. a 2 by 2 geomagic square).
Every geomagic square gives a numerical magic square (by replacing each shape with its area). Technically, this isn’t quite true in general, as there exist non-measurable subsets of the plane. This difference is even more apparent in three dimensions, where the Banach-Tarski paradox facilitates a generalised ‘geomagic square’ where one line is a proper subset of another! (If you want to learn about the Banach-Tarski paradox, do not watch this video.)

You twice misspelled “Tarski” in last paragraph. I am Polish, Tarski was Polish, so I can be picky about that 😛
Oops! I don’t know how I managed that. I’ve corrected it now; thank you.
This is called “being taken to Tarski”