This is a guest post by Gabriel Gendler. As such, any views expressed in this post do not reflect the views of Complex Projective 4-Space or of Adam P. Goucher.
In a recent post Adam P. Goucher recommended that readers adopt the Petersen graph as their favourite graph, if they had not chosen one already. This post is designed to promote an alternative favourite graph – the Rado graph.
Definition
We start with the following, seemingly tame, definition. Define the countably infinite graph 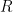 with vertex set
with vertex set  ; the edge set is
; the edge set is 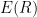 , and for
, and for  if and only if in the binary expansion of
if and only if in the binary expansion of  , the digit
, the digit 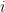 from the right is 1. So, for example,
from the right is 1. So, for example, 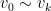 for odd
for odd 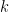 and
and 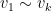 for
for  or
or  .
.
The extension property
First, we observe a useful but not immediately interesting property: for any finite disjoint sets of vertices  , there exists a vertex
, there exists a vertex 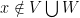 such that
such that 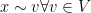 and
and 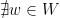 with
with  . The proof is constructive: let
. The proof is constructive: let 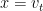 where
where  for
for 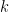 and large enough
and large enough  both in
both in 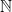 .
.
Induced subgraphs
Now we get our first impressive result. Every graph  with
with  countable is an induced subgraph of
countable is an induced subgraph of 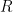 . For, supposing the vertices of
. For, supposing the vertices of  are labelled
are labelled 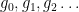 , we require an injective function
, we require an injective function 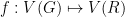 with
with 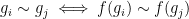 . Let
. Let 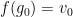 as a base case, with the inductive hypothesis that
as a base case, with the inductive hypothesis that 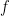 defined on
defined on 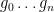 obeys the rule. Then for the inductive step we can find
obeys the rule. Then for the inductive step we can find  adjacent to precisely the correct vertices due to the extension property.
adjacent to precisely the correct vertices due to the extension property.
Uniqueness
Next things start to get weird, because it turns out that all countable graphs with the extension property are isomorphic. We will prove this by letting 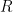 and
and  be two rival countable graphs with the extension property, and finding
be two rival countable graphs with the extension property, and finding 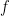 an isomorphism between them. We label the vertices of
an isomorphism between them. We label the vertices of 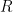 and
and  in the normal way and let
in the normal way and let  . Then supposing inductively that
. Then supposing inductively that 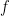 is legal and defined on
is legal and defined on 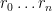 , and
, and 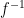 is defined on
is defined on 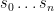 , we set values for
, we set values for  and
and 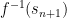 using the extension property if they haven’t already been set. Hence
using the extension property if they haven’t already been set. Hence 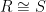 . We can also start with an isomorphism between any two induced subgraphs of
. We can also start with an isomorphism between any two induced subgraphs of 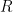 and build up the full isomorphism from there, so we find that the graph is symmetric and ultrahomogeneous.
and build up the full isomorphism from there, so we find that the graph is symmetric and ultrahomogeneous.
That was quite momentous. You may have seen it coming, but just like global warming that doesn’t stop this from being a big deal. As a consequence the weirdness becomes endemic.
Damaging the graph
Suppose 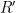 is obtained from
is obtained from 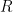 by deleting finitely many vertices and adding or deleting finitely many edges. Then
by deleting finitely many vertices and adding or deleting finitely many edges. Then 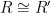 . This is a corollary of uniqueness; it is very easy to show that
. This is a corollary of uniqueness; it is very easy to show that 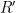 has the extension property (notice that in the proof of the extension property
has the extension property (notice that in the proof of the extension property 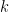 can be any integer so there are infinitely many legal
can be any integer so there are infinitely many legal  ).
).
That’s really weird. If the graph is subjected to GBH (or indeed initiated into a Cambridge drinking society) it retains its shape.
Tearing the graph into pieces
Equally weird is the following: If 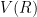 is partitioned into finitely many subsets
is partitioned into finitely many subsets  then at least one of the corresponding induced subgraphs is isomorphic to
then at least one of the corresponding induced subgraphs is isomorphic to 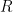 . This follows immediately from the case of a partition into two sets. For sets
. This follows immediately from the case of a partition into two sets. For sets 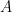 and
and 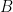 , suppose
, suppose 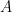 is not the Rado Graph. Then there are subsets
is not the Rado Graph. Then there are subsets 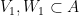 such that every
such that every  extending
extending  is in
is in 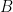 . Now for any subsets
. Now for any subsets  , there is an
, there is an  that extends
that extends  , and
, and 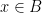 , so
, so 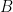 has the extension property. Hence either
has the extension property. Hence either 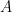 or
or 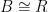 , so in the general case, for some
, so in the general case, for some 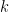 ,
,  .
.
Similarly, if the edges are 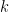 -coloured for finite
-coloured for finite 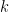 , then there exists an induced subgraph which is a 2-coloured Rado graph. The proof of this makes up the better part of a paper by Sauer and Pouzet which costs £30, so I won’t reproduce it here. However I will point out that this only needs to be proved for
, then there exists an induced subgraph which is a 2-coloured Rado graph. The proof of this makes up the better part of a paper by Sauer and Pouzet which costs £30, so I won’t reproduce it here. However I will point out that this only needs to be proved for 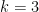 for the same reason as above.
for the same reason as above.
The Random Graph
Perhaps you’re sufficiently weirded out already. Perhaps you’ve found all the weirdness so far rather run-of-the-mill. Either way, I think you’ll agree that the next realisation is about as weird as they come.
We start with an empty, countably infinite graph. We pick any 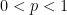 and we go through each pair of vertices, constructing an edge between them with probability
and we go through each pair of vertices, constructing an edge between them with probability 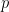 . The graph we get, independent of
. The graph we get, independent of 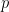 , is almost always (i.e. with probability 1) the Rado graph. This is actually easy to prove, using extension and uniqueness; for any set of vertices
, is almost always (i.e. with probability 1) the Rado graph. This is actually easy to prove, using extension and uniqueness; for any set of vertices 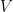 and
and 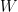 , and some vertex
, and some vertex  not in
not in 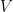 or
or 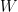 , the probability that
, the probability that 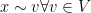 but
but 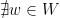 with
with  is positive, so taken over all possible
is positive, so taken over all possible  it is true with probability 1. Since
it is true with probability 1. Since 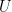 and
and 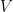 are finite, the number of pairs of subsets is countable, and the intersection of countably many events each with probability 1 is 1, as required.
are finite, the number of pairs of subsets is countable, and the intersection of countably many events each with probability 1 is 1, as required.
At this point, the weirdness is so intense that it threatens to destroy the universe as we know it. Things fall apart at the seams. It turns out that the moon is made of cheese; China withdraws unilaterally from Tibet and voluntarily cedes all authority to Taipei. The Israeli government and the Palestinian Authority sign a peace treaty implementing a one-state solution, and the new country is known as the Federal Republic of Integral Bananas. Americans vote unilaterally to ban the ownership of firearms in a referendum, and scientists discover a cure for cancer whose active ingredient is powdered chocolate. Finally, every member of the IMO team gives up maths and enrols at Oxford for an undergraduate degree in History of Art. Why? Because the random graph on  vertices is in fact the not-very-random-at-all graph.
vertices is in fact the not-very-random-at-all graph.
Alternative Constructions
Now that the Rado graph has ripped the universe apart it can sit back and just show off for a bit. Here are two alternative constructions of 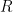 ; both can be verified using the extension property and are set as an exercise for the reader.
; both can be verified using the extension property and are set as an exercise for the reader.
- Let the vertex set be all primes
. Put
. To verify this you need to understand the basics of quadratic reciprocity and Dirichlet’s theorem.
- Let
be universal; that is, writing
as a string of 0s and 1s in the natural way, every finite string of 0s and 1s can be found in
. Then let the vertex set be
and put
. This one can be proved without any further knowledge.
Proving stuff about this graph is quite easy
Everything we’ve seen has been quite easy to prove. That’s what I like about the Rado graph; the definition is such that everything else just falls into place. To convince yourself of this, why not find a few simple properties of the Rado graph, such as its chromatic number, its diameter and its complement? Does there exist a Hamiltonian path through every vertex? In a cops and robbers game where the robber takes it in turns with n cops to move to an adjacent vertex (all the cops move at once), who wins? Everything seems to come straight out of the definition of the Rado graph.
Why you should adopt the Rado graph as your favourite graph
A favourite graph is most useful for testing hypotheses. As such, the Rado graph is an excellent choice of favourite graph because of three features that make it a good candidate for answering hypotheses in the negative. These are:
- It is easy to work with. The immense symmetry, the extension property, the subgraph property and the uniqueness of the Rado graph make it very easy to prove things about it. Therefore it will ordinarily be easy to check whether a hypothesis is true for the Rado graph (see previous paragraph).
- It has strange properties. This makes it feasible that the Rado graph should provide a much better answer to a problem than any other graph.
- It is unusual. Suppose you were to bump into your friends as they struggle to prove or disprove some graph-theoretic hypothesis, and the Rado graph provides a counterexample. You can look forward to several minutes of sincere respect for such an elegant yet obscure solution. On the other hand, if your favourite graph is the complete graph on three vertices, and that provides a counterexample, then it’s probable that your friends will already have answered their hypothesis by the time you arrive. Moreover, if you are in time to use
as a counterexample, your solution will be met not with awe or respect, but with disappointment and embarrassment. The same goes for any exams; if a well-known counterexample exists, the hypothesis is unlikely to be set as a question, whereas it’s not unlikely that the Rado graph should provide a counterexample.
“But I’ve already got a favourite graph!”
I recognise that many people are already in a relationship with a graph, especially since those who were single a few weeks ago probably hooked up with the Petersen graph after being introduced to it by Adam. Nevertheless there are likely to be readers without one, either because they had a bad first date with the Petersen graph, or because they have broken up since then due to the inevitable disappointing relationship that followed those dream-like first few moments. Additionally, it’s probable that some readers didn’t see that post, in which case they might still be virgins. Finally, those in a relationship with the Petersen graph might be ready to move on; indeed, it is rather promiscuous (by which I mean overused), and just as any partner ought not to sleep around, so a favourite graph ought to be unusual. If, on the other hand, you are happily married to the Petersen graph, perhaps you might want to adopt the Rado graph as your favourite infinite graph. If the Petersen graph is insulted, remind it that the Rado graph contains infinitely many copies of the Petersen graph.
Sources
http://www.math.unt.edu/~mpc0061/logicgroup/randomgraph.pdf
http://en.wikipedia.org/wiki/Rado_graph
http://mabit.org.hu/~p_erdos/1963-04.pdf
http://en.wikipedia.org/wiki/Rado_graph
http://mabit.org.hu/~p_erdos/1963-04.pdf

Gabriel, what am I supposed to do if the problem concerns finite graphs only?
Also, I believe there was a talk at Trinity about this at some point – was it the 2011 Pre-IMO camp, Adam?
Of course, I can’t answer your second question. Regarding your first, I suppose that will always be a problem; for example, if your favourite graph is the Petersen graph you will be disappointed if the question is about planar graphs. No graph can possibly be applicable in every situation.
I, however, can answer your second question: yes, and it was by Bryn Garrod. I think that Gabriel’s article has more detail, though, about the Rado graph; Garrod’s talk also alluded to the fact that there are lots of uncountable random graphs.
Also, I agree that no graph is applicable to all situations. Most of the false solutions in the FST 2013 graph theory question made erroneous assumptions about planar graphs, which fail for the octahedral graph and (even more spectacularly) fail for the icosahedral graph.
Great article, Gabriel!
By the way, my condolences go out to those people whose favourite graph is the 57-regular Moore graph, not knowing whether or not it actually exists.
I second your opinion on the article. 🙂
Aren’t you just sending out condolences to yourself here though…?
No, my favourite is the Petersen graph, as I alluded to in the article about the Hoffman-Singleton graph.
https://www.youtube.com/watch?v=kQFKtI6gn9Y
May I draw your attention to a comment made by you at 18:28 yesterday evening:
“(My favourite graph is the 57-regular Moore graph, by virtue of it being unknown whether or not it actually exists. 😛 )”
;P
I can’t speak for Adam but the smiley indicates that the comment was light-hearted. And for the record, I could be arguing in my spare time.
He’s right, you know.
Pingback: Ten things you (possibly) didn’t know about the Petersen graph | Complex Projective 4-Space