On an infinite square lattice, the B36/S125 cellular automaton proceeds similarly to Conway’s Game of Life (B3/S23), but with different birth and survival conditions. Specifically, a dead cell becomes live if surrounded by 3 or 6 live neighbours, and a live cell survives if surrounded by 1, 2 or 5 live neighbours. As usual (c.f. question 9), each cell dies unless specified otherwise.
The dynamics are not as interesting as the Game of Life, although there is a naturally-occurring glider and related infinite-growth pattern (discovered by Nathaniel Johnston during a massive search with random initial conditions):

One of the more interesting properties of the cellular automaton is that if the universe is composed entirely of 2 × 2 blocks in a square lattice arrangement, this will be the case for all time. We can think of B36/S125 as emulating a simpler cellular automaton:
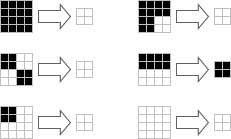
This cellular automaton is slightly unusual in that the cells are in different positions in odd generations and even generations. A spacetime diagram of this gives truncated octahedral cells in a configuration known as the body-centred cubic lattice:
For want of a better term (block cellular automaton is slightly ambiguous, and can refer to the similar — albeit distinct — concept of a Margolus neighbourhood), I shall henceforth refer to these as BCC automata. Nathaniel Johnston investigated rectangular oscillators in the BCC automaton arising from B36/S125, showing how they in turn emulate an even simpler (one-dimensional) cellular automaton, namely Wolfram’s Rule 90. It transpires that this behaviour was investigated earlier by Dean Hickerson on the notorious Usenet group, comp.theory.cell-automata.

Oscillators of periods 6 (2^3 – 2) and 14 (2^4 – 2) in the B36/S125 cellular automaton.
Emulation can go in the opposite direction. For a cellular automaton such as Life, we can arbitrarily group the cells into 2 × 2 blocks, thus enabling it to be emulated in a 16-state BCC automaton. This is used as the base case for Bill Gosper’s algorithm HashLife, which uses hashed quadtrees to simulate patterns frighteningly quickly.

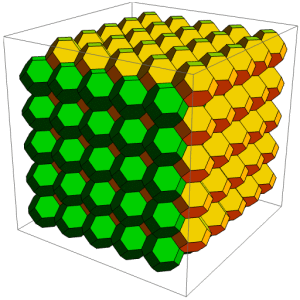
> This is used as the base case for Bill Gosper’s algorithm HashLife…
I just looked at the BCC-emulates-Life case until I understood it (or thought I did). Here’s a detail that isn’t quite clear from the description. Let’s say you’re emulating a small still life in Conway’s Life, such as a block. The block will be a spaceship rather than a still life in BCC-space — it will end up moving one BCC-cell diagonally every two ticks (in some arbitrarily-chosen direction).
Is that right? Or is there some way to make the emulated still life actually sit still in BCC-space… without going so far as using different 16-state BCC automata for even and odd generations?
[Answering my own confusion –]
Ah, no, I think I see it now. If each new generation had to be on a square grid lined up with the previous generation, you’d have to choose some arbitrary offset direction — but on a body-centered-cubic lattice, there’s a place for each new cell “in the corners”, so to speak, of the four previous cells.
The grid is partitioned into different 2×2 blocks in odd and even generations — dual tilings, to be specific — rather like the Margolus neighbourhood. So, a block in GoL would be alternately represented by 1 cell and 4 cells (or 2 cells and 2 cells, depending on the position).
Greaat blog you have here