A fascinating paper by Louis Kauffman establishes the equivalence of the four-colour theorem (the assertion that any planar graph can have its vertices coloured with one of four colours, such that neighbouring vertices have different colours) to the following seemingly unrelated combinatorial statement:
- Let n be a positive integer, and let A and B be two complete parenthesisations of the expression
, where × is the three-dimensional cross product. Then we can assign each of
to be either i, j or k such that the two expressions are non-zero and equal.
Moreover, the proof is not particularly complicated. Firstly, we shall examine other restatements of the four-colour theorem.
Vertex, face and edge colourings
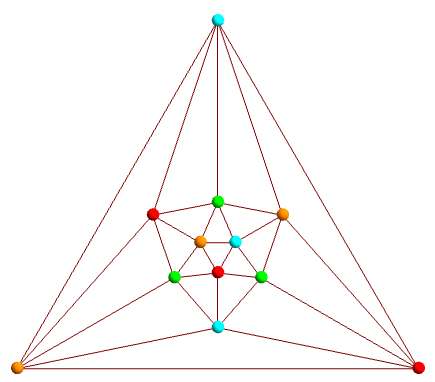
In its simplest form, the four-colour theorem states that we can colour the vertices of a planar graph with at most four colours, such that no adjacent vertices have the same colour. For example, take the graph of the icosahedron, which is indeed planar:
Tait proved that this is equivalent to the statement that every bridgeless planar 3-regular graph can have its edges coloured with three colours, such that every vertex is incident with precisely one edge of each colour. It’s not too difficult to reconstruct the intermediate steps without ever having seen the proof, just by knowing the two propositions and by employing reasoning.
Firstly, note that Tait’s statement is about planar graphs where every vertex has degree 3. Conversely, the worst-case scenario of the original statement is where every face is a triangle (since any planar graph can be ‘triangulated’ into this form). Hence, a good idea is to form the planar dual of the worst-case scenario of the original statement:
We can colour the faces of a 3-regular plane (or spherical) graph with four colours, such that no two faces of the same colour share a common edge.
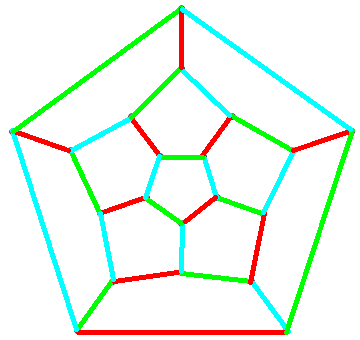
The 4-colouring of the vertices of the icosahedral graph, for instance, is equivalent to the following 4-colouring of the faces of the dodecahedral graph:
Now, to convert this to a 3-colouring of the edges, we want to somehow assign a colour to an edge based on the colours of the neighbouring regions, and to do this in a nicely reversible way. To do so, let the regions be coloured with elements of the Klein 4-group, and the edges be coloured by the product of the two regions. Since it’s Abelian and every element is its own inverse, we obtain a colouring of the edges with the non-identity elements of the Klein 4-group. Supposing that yellow is the identity, we get the following edge-colouring:
This establishes the equivalence of the four-colour theorem and Tait’s restatement. Not too difficult, was it? Now, we can start to see the similarity with Kauffman’s combinatorial problem. If we ignore the signs of the vectors, then the colours of these edges can be the three unit vectors i, j, k, and the vertices correspond to the cross product operation. Parenthesisations are equivalent to binary trees, so (temporarily ignoring signs) Kauffman’s combinatorial problem is just Tait’s restatement applied to the special case of graphs obtained from gluing two equally-sized trees together.
Dealing with signs
One of the subtleties is that it is not immediately obvious that we would necessarily get A = B, rather than A = −B. To overcome this, Kauffman employed an idea by Roger Penrose of assigning either i or −i (complex numbers, not quaternions or unit vectors!) to each vertex, depending on whether the colours of the three edges are arranged in clockwise or anticlockwise order. Then, Kauffman shows that the product of the vertices is 1, which is equivalent to the signs working out correctly.
Proofs of the four-colour theorem
The first correct proof of the four-colour theorem was Appel and Haken’s massive case-bash, which relied on machine-checking each of 1936 configurations for reducibility. Essentially, they proved that any counter-example to the four colour theorem could be reduced to a smaller counter-example, so by induction the theorem is true.
Recently, a proof was announced of the snark conjecture, that any snark (bridgeless 3-regular graph with no 3-edge-colouring) must contain the Petersen graph as a minor. This is clearly a generalisation of Tait’s restatement of the four-colour theorem, which is the contrapositive of ‘no snark is planar’. The Petersen graph is both the simplest snark and the first to be discovered.
The Petersen graph is also a forbidden minor for the set of linklessly embeddable graphs (those which cannot be drawn in three-dimensional space without two cycles forming a Hopf link), so it follows that any bridgeless linklessly embeddable 3-regular graph must have a 3-edge-colouring, generalising Tait’s restatement of the four-colour theorem.
The proof of the snark theorem is largely unpublished, although apparently it is another computer-assisted proof. Hence, it (unfortunately!) does not provide a counter-example to Doron Zeilberger’s ultimate fantasy of the four-colour theorem having no ‘human’ proofs.


Pingback: Ten things you (possibly) didn’t know about the Petersen graph | Complex Projective 4-Space
Pingback: W. T. Tutte | Complex Projective 4-Space
Pingback: Punting in clearings of arbitrarily small Lebesgue measure | Complex Projective 4-Space
Wholesale Youth nfl Jerseys For Sale Fast Free Shipping
Pingback: Descartes snark | Complex Projective 4-Space