The 50-pence and 20-pence coins are regular curvilinear heptagons, where each edge is a circular arc centred on the opposite vertex.
One may ask why the coins have such an unusual shape. One possible answer is that it is impossible for a counterfeiter to forge with just a compass, straightedge and sheet of cupronickel. However, since compass-and-straightedge constructions are seldom used in practice, this is clearly not the reason.
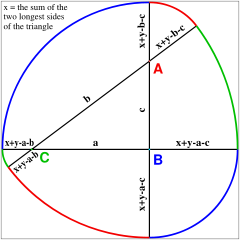
This curvilinear heptagon has another property, which is easiest to demonstrate with its triangular analogue, the Reuleaux triangle. It is a curve of constant width, which means that all of its axonometric shadows are line segments of equal width. Equivalently, when rolled on a flat surface, the height of the coin remains constant.
The reason for employing a curve of constant width is that it can be more easily recognised by mechanical coin-detecting machines. The Reuleaux polygons are not the only curves of constant width, however, since we can easily design irregular curvilinear polygons with this property. Again, these are all piecewise circular.
The next question is whether there exist curves of constant width which are not piecewise circular. Intuitively, the answer is yes, since it seems plausible that a limiting process could be applied where the lengths of the circular arcs tend to zero. A more rigorous formulation is given by the following system of differential equations, where (as functions of t) are the endpoints of the line:
- a × k = b × k = 0 (both endpoints lie in the ij-plane);
- a’ · (a − b) = b’ · (b − a) = 0 (the endpoints move perpendicularly to the line segment, preserving its length);
- a’ × (a − b) · k ≥ 0 and b’ × (b − a) · k ≥ 0 (the endpoints move in the same direction);
- a(t + T) = b(t) and b(t + T) = a(t) (the curve is closed).
It transpires that there are algebraic curves other than the circle, which have constant width. One example is a degree-8 curve discovered by Stanley Rabinowitz.
Solids of constant width
The obvious generalisation of the Reuleaux triangle to three dimensions, the Reuleaux tetrahedron, does not have constant width. Nevertheless, Meissner demonstrated that it is possible to modify three of the edges of the tetrahedron to yield an actual surface of constant width, the Meissner tetrahedron.
Meissner tetrahedra can be obtained commercially from Maths Gear.


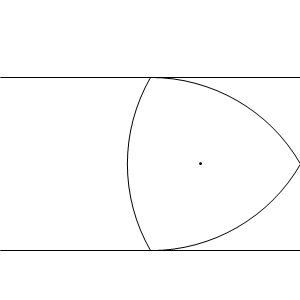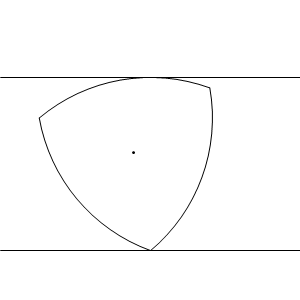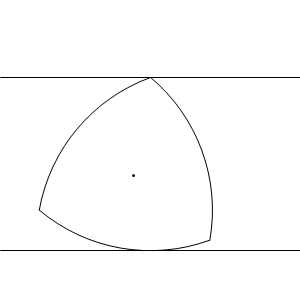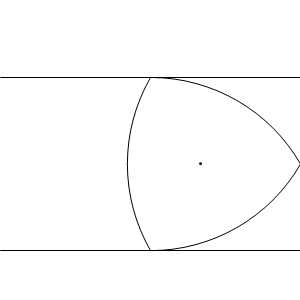
Reuleaux triangles are used to drill square holes
Indeed. Technically, it’s a square with slightly rounded corners, but nevertheless much better than the circle or any other Reuleaux polygon.
Pingback: Constant Width Objects - Not Spheres!
Pingback: Denser packing of pound coins discovered | Complex Projective 4-Space