You are probably familiar with the Riemann hypothesis. This concerns the behaviour of the Riemann zeta function, which is defined on the complex plane by analytic continuation of the following series:
The behaviour of the zeroes of the function outside the strip is well-known: they are precisely at the even negative integers. The Riemann hypothesis states that within this strip, the only zeroes have real part exactly equal to ½. It is customary to include, at this point, an entirely gratuitous plot of the real part of the zeta function near the origin:
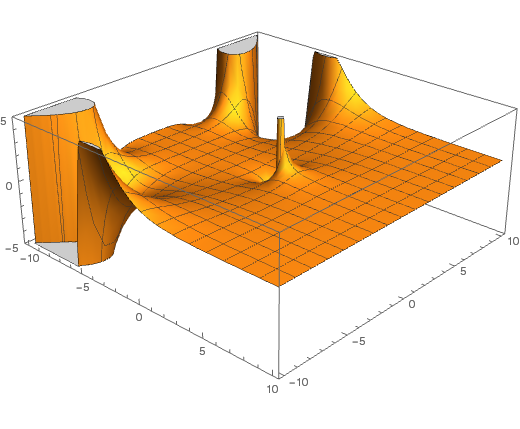
Whilst interesting enough for the Clay Mathematics Institute to offer a prize of USD for its resolution, the generalised Riemann hypothesis has far more far-reaching implications. This states that for every Dirichlet L-function, all of its zeroes within the critical strip have real part exactly equal to ½. Since the Riemann zeta function is the simplest example of a Dirichlet L-function, the ordinary Riemann hypothesis is subsumed by the generalised Riemann hypothesis.
What is a Dirichlet L-function?
A Dirichlet L-function is specified by a positive integer k and a completely multiplicative function satisfying:
- χ(n) = 0 if and only if gcd(n, k) ≠ 1;
- Periodicity: χ(n + k) = χ(n) for all integers n;
- Complete multiplicativity: χ(m) χ(n) = χ(mn) for all integers m, n.
Given such a Dirichlet character χ (there are finitely many choices, namely φ(k), for any given k), the corresponding L-function is defined as:
When k = 1, the unique Dirichlet character is the constant function 1, whence we recover the original Riemann hypothesis.
Knottedness is in NP, modulo GRH
This is the title of a very interesting paper by Greg Kuperberg. It has been proved that an unknotted knot diagram can be disentangled into a simple closed loop in a number of Reidemeister moves polynomial in the number of crossings in the original diagram. It follows that unknottedness is in NP, as an optimal disentangling sequence is a polynomial-time-checkable certificate of unknottedness.
Kuperberg’s paper proves that unknottedness is in co-NP, i.e. knottedness is in NP. However, the proof relies on the unproven generalised Riemann hypothesis in a very interesting way. Specifically, if the fundamental group of the complement of the knot is non-Abelian — as is the case for any non-trivial knot — then it has a non-Abelian representation over SU(2). If the generalised Riemann hypothesis holds, it is possible to find a reasonably small prime p for which there is such a modulo-p representation; in this case, the images of the generators under this representation (expressed as 2-by-2 matrices with entries modulo p) form a certificate for knottedness. It then suffices to check that they do not all commute, and that they satisfy the relations of the knot group presentation.
ab + bc + ca
Which positive integers cannot be expressed in the form ab + bc + ca, where a, b, c are positive integers? There are either 18 or 19 such numbers, the first 18 of which are enumerated in A025052:
1, 2, 4, 6, 10, 18, 22, 30, 42, 58, 70, 78, 102, 130, 190, 210, 330, 462
There may be a 19th such number, which must necessarily be greater than 10^11, and can only exist provided the generalised Riemann hypothesis is false. In particular, Jonathan Borwein proved that the existence of this 19th number requires a Dirichlet L-function to have a Siegel zero, which would contradict GRH.
The positive integers inexpressible in this form with a, b, c distinct positive integers are called idoneal numbers, and there are either 65 or 66 of them. The 65 known examples are sequence A000926:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, 16, 18, 21, 22, 24, 25, 28, 30, 33, 37, 40, 42, 45, 48, 57, 58, 60, 70, 72, 78, 85, 88, 93, 102, 105, 112, 120, 130, 133, 165, 168, 177, 190, 210, 232, 240, 253, 273, 280, 312, 330, 345, 357, 385, 408, 462, 520, 760, 840, 1320, 1365, 1848
Idoneal numbers have an equivalent definition of being the positive integers D such that any number uniquely expressible in the form , with
and
coprime, is necessarily either a prime, a prime power, or twice a prime power.
Deterministic Miller-Rabin
The fastest known deterministic algorithm for determining if a number is prime is AKS, which takes time . This is, unfortunately, rather slow.
The Miller-Rabin probabilistic test tells you whether a number is prime in time . If the number is prime, it correctly claims that it is prime. If it is composite, however, it can lie with probability 1/4. In practice, running this test with many randomly-chosen initial parameters will give a result with sufficiently high probability that it is useful in practice (e.g. in cryptography).
Assuming GRH, it can be shown that applications of Miller-Rabin are sufficient to guarantee primality, and therefore that there exists a deterministic algorithm with running time
, noticeably faster than AKS. The Shanks-Tonelli algorithm for finding square-roots modulo a prime will also run deterministically in polynomial time as a result of the same idea.
Artin’s conjecture on primitive roots
This states that every integer a which is neither −1 nor a perfect square is a primitive root modulo infinitely many primes. In 1967, Hooley proved this conditional on the Generalised Riemann Hypothesis, establishing that the set of primes for which a is a primitive root has positive density (among the set of all primes).

Pingback: Sorting networks | Complex Projective 4-Space
GOD ALMIGHTY’S GRAND UNIFIED THEOREM NICKNAMED GAGUT Gij,j=0 REPRESENTS THE GOD ORDER/NEWS ORDAINING PROF. G. OYIBO (A BLACK MAN) WITH THE ULTIMATE INTELLIGENCE AND HENCE THE BLACK PEOPLE MOST INTELLIGENT AND UNDEFEATABLE RACE. GOD has ordained a Black Man Prof. G Oyibo with the ultimate intelligence Eta sub infinity, where Eta sub n exactly represents intelligence, and “n” the level of intelligence which GOD designed for Prof. G. Oyibo “n” to be Infinity, hence eta sub infinity. Since Black People share the same genes as Prof. G. Oyibo, GOD has now re-ordained the Black Race to be the Most Intelligent, Richest and Undefeatable Race. GOD ALMIGHTY’S GRAND UNIFIED THEOREM nicknamed GAGUT is a revelation from GOD which infallibly proved that all theorems (also called everything that exists) and all equations, also called morphisms, past present and future, originate out of one invariant Gi defined as GOD with orthogonal components Gij, and a divergence (also called change) of Gij,j=0. Let me go over that again, GOD ALMIGHTY’S GRAND UNIFIED THEOREM nicknamed GAGUT is a revelation from GOD which infallibly proved that all theorems (also called everything that exists) and all equations , also called morphisms (which can mean isomorphisms or polymorphisms), past present and future, originate out of one invariant Gi, defined as GOD
Pingback: Atiyah’s problem | Complex Projective 4-Space
So I find people linking to your webpage as an “expert” on the upcoming work of Atiyah… who links to their own post on the GRH and then fails to actually state the GRH correctly. The GRH is a statement not only for L-functions associated to Dirichlet characters (which is what you write) but to L-functions for all Artin representations of number fields. (To put it a different way not all Dirichlet L-functions are associated with characters which is what you seem to believe.) To deduce the Artin primitive root conjecture you need GRH for the L-functions of number fields associated to fields of the form Q(zeta_n,a^(1/n)) for all n which are not in general abelian. You truly are an insufferable prat. Delete this comment if you want but at least correct the fucking post just in case someone with half a brain ends up here and wants to actually learn something.
I love this so much it makes my penis hurt!
I am also finding that the excitement here is so great it my penis hurt!