Moritz Firsching asked in 2016 whether there exists a dodecahedron, combinatorially equivalent to a regular dodecahedron, with rational vertices lying on the unit sphere. The difficulty arises from the combination of three constraints:
- The twelve pentagonal faces must all be planar;
- The vertices must all be rational points;
- The vertices must all lie on the unit sphere.
Conditions 1 and 2 are realised by Schulz’s dodecahedron (shown in Firsching’s question). Conditions 1 and 3 are realised by a regular dodecahedron. But finding a solution that satisfies all three conditions simultaneously turns out to be hard. A computer-assisted search only found a single example, up to Möbius transformations of the unit sphere:
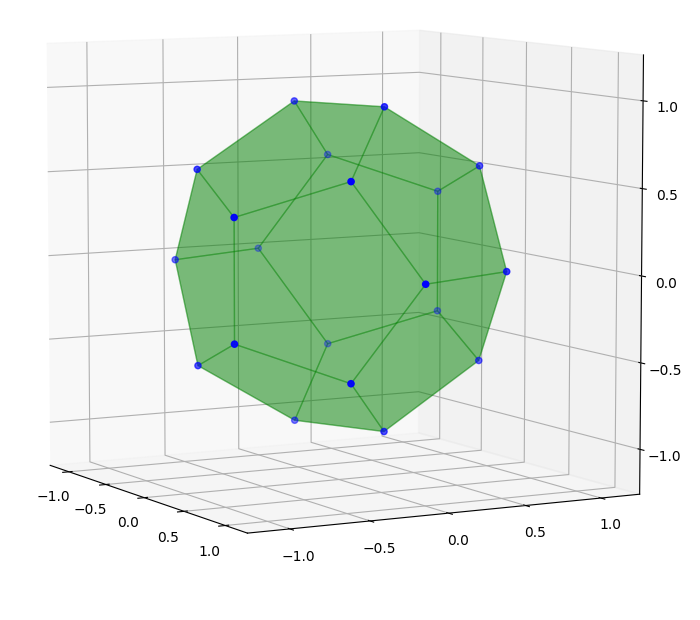
The vertices are obtained from the following set of integer lattice points:
iverts = [[ 1840720, 1798335, 0], [ 2573375, 0, 0], [ 773500, 1963500, -1472625], [ 773500, 1963500, 1472625], [ 794070, 323510, -2426325], [ 794070, 323510, 2426325], [ 905828, -2223396, -926415], [ 905828, -2223396, 926415], [ 1925420, -863940, -1472625], [ 1925420, -863940, 1472625], [-1840720, -1798335, 0], [-2573375, 0, 0], [ -773500, -1963500, 1472625], [ -773500, -1963500, -1472625], [ -794070, -323510, 2426325], [ -794070, -323510, -2426325], [ -905828, 2223396, 926415], [ -905828, 2223396, -926415], [-1925420, 863940, 1472625], [-1925420, 863940, -1472625]]
by dividing everything by 2573375. The planarity of the pentagonal faces and the fact that the points lie on a radius-2573375 sphere are checked by this notebook.
The dodecahedron has an order-8 symmetry group (it has three orthogonal planes of reflectional symmetry) and is visually very close to being regular. The symmetry group was a consequence of the search methodology; I specifically looked for solutions with this symmetry group in order to narrow down the search space.
By polar reciprocation, this also answers the equivalent question: ‘does there exist an icosahedron with rational vertices that contains an inscribed unit sphere?’
Methodology
Subject to the points being on the unit sphere, the planarity is equivalent to concyclicity. After stereographically projecting the unit sphere to the plane, which preserves rationality of points, the problem becomes:
Does there exist an embedding of the dodecahedral graph into the plane, with each vertex being a rational point, such that the five vertices of each face are all concyclic?
I restricted attention to symmetrical solutions invariant under reflection in each of the coordinate axes and under inversion in a circle centred on the origin:
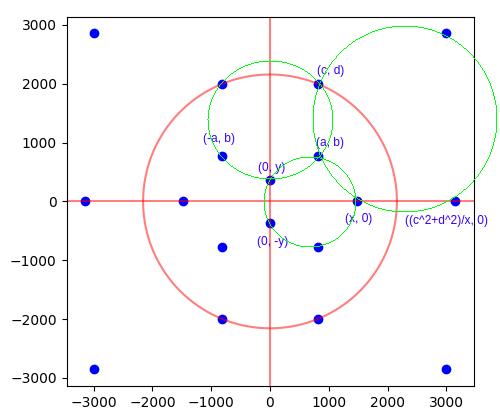
(Note that the two points furthest from the origin are not shown in the above diagram.)
Here the red lines and circle are the axes of reflection and inversion, respectively. The three green circles are the necessary concyclicities, implying that the other nine pentagons are also concyclic by symmetry. These can be translated into Diophantine equations by using the fact that the four points {(x1, y1), (x2, y2), (x3, y3), (x4, y4)} are concyclic or collinear if and only if the following 4-by-4 determinant vanishes:
- 1, x1, y1, x1² + y1²;
- 1, x2, y2, x2² + y2²;
- 1, x3, y3, x3² + y3²;
- 1, x4, y4, x4² + y4²;
I wrote a program to search over integer values of a,b,c,d and check whether the values of x and y implied by the upper-right and upper-left green circles, respectively, are rational. If so, the program proceeds to check that the remaining (lower) green circle holds; if so, it reports a solution. The program reported several solutions, but they were all scalar multiples of a single ‘primitive’ solution and therefore correspond to the same polyhedron.
Do there exist any more solutions?
My search program (available here) only found a single primitive solution, even when the threshold was increased to N = 1000. This is not particularly conclusive: it’s often the case that Diophantine equations have solutions that are very few and far between, even if there are infinitely many solutions; the Pell equation is a simple example of this phenomenon.
EDIT: after running on a GPU with N = 10000, another two primitive solutions emerged.
Of course, if history is any guide, it’s entirely likely that Noam Elkies will storm in at any moment wearing a superhero cape and brandishing an infinite family of solutions to this problem.

I thought I’d stop waiting for the superhero cape wearing Noam Elkies to brandish his infinite solutions, and have a go at the problem myself. :p
What I’ve found so far is that the three equations given by the vanishing of the 4×4 determinants are surprisingly simpler than is obvious from first glance. Many factors drop out of the equations, factors which if set to zero result in highly degenerate solutions, specifically the circle collapsing onto it’s axis of symmetry.
The upper right circle equation drops a factor of c^2+d^2-a^2-b^2, which if zero would result in massive degeneracies due to the point (a, b) then being on the circle of inversion. This results in a homogeneous quartic equation in a, b, c, d, and x.
The upper left green circle results in a quartic equation in a, b, c, d, and y. However, the factor 2a is throughout the equation, so we can divide through by that (if a=0 points collapse onto the y axis), to get a homogeneous cubic equation in a, b, c, d, and y.
Similarly, the lower green circle results in a quartic equation, with 2b dropping out as a factor. This results in a homogeneous cubic equation in a, b, x, and y.
While the problem is still highly nontrivial, it seems less completely intractable now. We just have two cubics and a quartic intersecting in projective 6-space.
I suspect the order 8 symmetry you have forced the solutions to have is the reason behind these dramatic reductions in order, and that further work would reveal other benefits from the symmetry group.
I can give the equations and derivations on request, but it is a simple (if tedious) exercise to derive them from the determinant condition for concyclicity.
I’d like to have them, since I also want to have a try at it, I don’t really enjoy algebra, and Wolfram|Alpha is refusing to cooperate right now.
Thanks! 🙂
Also somehow I got a factor of -x^2(-c^2-d^2+x^2) from the upper right circle. Is it correct?
Pingback: Another two rational dodecahedra | Complex Projective 4-Space
Pingback: Infinitely many rational dodecahedra | Complex Projective 4-Space